§3 线性变换
一、基本概念
[线性变换] 设![]() 和
和![]() 是同一域F上的两个线性空间,映射
是同一域F上的两个线性空间,映射![]() 满足下面两个条件:
满足下面两个条件:
(i) ![]() ,对任意
,对任意![]() ;
;
(ii) ![]() ,对任意
,对任意![]() ;
;
则称L为线性映射或线性变换,又称同态. 若![]() 与
与![]() 是同一线性空间,则称L为空间V到自身的线性变换,或称为自同态.
是同一线性空间,则称L为空间V到自身的线性变换,或称为自同态.
例1 在一个线性空间V上的一个线性函数(见本节三)![]() 是V到域F(考虑为一维线性空间)的一个线性变换.
是V到域F(考虑为一维线性空间)的一个线性变换.
例2 设![]() 是线性空间V上的线性函数,则由
是线性空间V上的线性函数,则由
所确定的映射是V到m维空间![]() 的一个线性变换.
的一个线性变换.
例3 设V是区间[a,b]上所有连续函数组成的实线性空间. 若令
则L就是V的一个线性变换. 事实上,因为对任意实数b,c,有
例4 设V为一切实系数多项式f(x)组成的线性空间. 若令
![]() (
(![]() 为
为![]() 的导数)
的导数)
则L是V的一个线性变换.
[线性变换的性质]
1o线性变换定义中的条件(i),(ii)等价于:对任意![]()
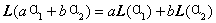
重复应用这公式,导出
2o若![]() 是线性无关的,
是线性无关的,![]() 是一个线性变换,则
是一个线性变换,则
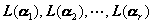
也是线性无关的.
3o若![]() 构成V的一个基底,又设
构成V的一个基底,又设![]() ,则唯一地存在一个线性变换L,使
,则唯一地存在一个线性变换L,使
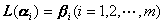
[零变换·恒等变换·逆变换] 将线性空间V的任一矢量α都变为线性空间![]() 的零矢量的变换,称为零变换记作O. 即对任一
的零矢量的变换,称为零变换记作O. 即对任一![]() ,有
,有
![]() (
(![]() 为
为![]() 的零矢量)
的零矢量)
将线性空间V中任一矢量α都变为自己的变换,称为恒等变换.
记作I,即对任一![]() ,有
,有
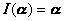
零变换和恒等变换都是线性变换.
对![]() 的线性变换L,若存在
的线性变换L,若存在![]() 上的线性变换M,使
上的线性变换M,使![]() ,则称M为L的逆变换,记作
,则称M为L的逆变换,记作![]() .
.
[线性变换的矩阵] 设![]() 是线性空间V的一组基底,
是线性空间V的一组基底,![]() 是
是![]() 的基底,
的基底,![]() 是线性变换,那末
是线性变换,那末![]() 可表为
可表为
由系数所组成的矩阵
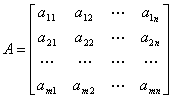
称为线性变换L关于基{![]() }和{
}和{![]() }的矩阵.
}的矩阵.
特别,当V与![]() 的维数相同,或L是V自身的线性变换,则A为方阵.
的维数相同,或L是V自身的线性变换,则A为方阵.
在基底确定之后,线性变换和它的矩阵建立了一对一的对应关系. 零变换的矩阵是零矩阵,恒等变换的矩阵是单位矩阵.
[线性变换的特征值与特征矢量] 如果存在![]() ,使得自同态
,使得自同态![]() 满足
满足
那末称![]() 为线性变换L的特征值(特征根),称
为线性变换L的特征值(特征根),称![]() 为对应于
为对应于![]() 的特征矢量.
的特征矢量.
一个线性变换的特征值与特征矢量分别等于该变换的矩阵的特征值与特征矢量.
[象·象源·核·线性变换的秩] 若![]() 是一个线性变换,则称
是一个线性变换,则称![]() 为V的象,称V为象源,称
为V的象,称V为象源,称![]() 为核.
为核. ![]() 的维数称为L的秩,
的维数称为L的秩,![]() 的维数称为退化次数.
的维数称为退化次数.
一个线性变换![]() 的核
的核![]() 与象
与象![]() 分别为V和
分别为V和![]() 的线性子空间,核的维数与象的维数之和等于象源的维数. 即
的线性子空间,核的维数与象的维数之和等于象源的维数. 即
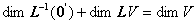
一个线性变换的秩等于该变换的矩阵的秩.
