三、拉格朗日插值多项式
[拉格朗日插值公式] 已知单变量函数![]() 的n+1个节点
的n+1个节点![]() 及其对应的函数值
及其对应的函数值![]() ,对于插值区间内任一点x,可用下面拉格朗日插值多项式
,对于插值区间内任一点x,可用下面拉格朗日插值多项式![]() 计算函数值∶
计算函数值∶
![]()
这里 ![]()
![]()
特别对于等距节点![]()
![]()
![]() ,有
,有
![]()
![]()
式中 ![]()
[埃特金逐步计算法]
已知![]() ,求插值区间内任一点a的拉格朗日多项式的数值
,求插值区间内任一点a的拉格朗日多项式的数值![]() ,可按下表从左到右逐列进行计算。
,可按下表从左到右逐列进行计算。
|
|
|
|
|
|
|
… |
|
|
|
|
|
|
|
|
|
… |
|
|
表中![]() 表示用
表示用![]() 作节点的一次插值多项式;
作节点的一次插值多项式;![]() 表示节点为
表示节点为![]() 的一次插值多项式;一般
的一次插值多项式;一般![]() 表示节点为
表示节点为![]() 的k次插值多项式。表中左起第四列以后的各列都是对应的插值多项式在a点的数值,它们之间有下面的关系:
的k次插值多项式。表中左起第四列以后的各列都是对应的插值多项式在a点的数值,它们之间有下面的关系:

![]()

![]()
………………………………………………………
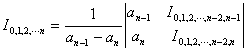
利用拉格朗日插值多项式计算某一点a的数值时每增加一个节点,必须按公式重新计算,而埃特金逐步计算法避免了这个缺点。