|
|
|
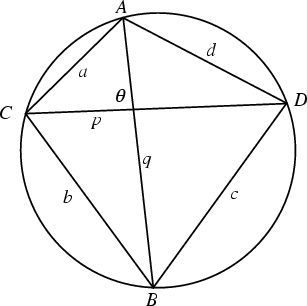
A Quadrilateral for which a Circle can be circumscribed so that it touches each Vertex. The Area is then given by a special case of Bretschneider's Formula. Let the sides have lengths
![]() ,
, ![]() ,
, ![]() , and
, and ![]() , let
, let ![]() be the Semiperimeter
be the Semiperimeter
| (1) |
| (2) | |||
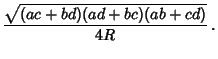 |
(3) |
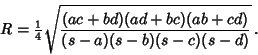 |
(4) |
| (5) |
| (6) |
| (7) |
| (8) |
The Area of a cyclic quadrilateral is the Maximum possible for any Quadrilateral with the given
side lengths. Also, the opposite Angles of a cyclic quadrilateral sum to ![]() Radians (Dunham 1990).
Radians (Dunham 1990).
A cyclic quadrilateral with Rational sides ![]() ,
, ![]() ,
, ![]() , and
, and ![]() , Diagonals
, Diagonals ![]() and
and ![]() , Circumradius
, Circumradius ![]() , and Area
, and Area ![]() is given by
is given by ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() .
.
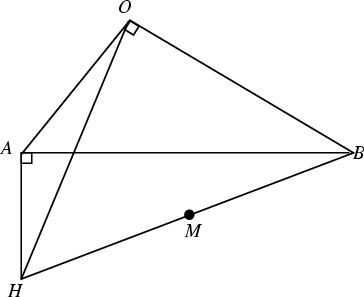
Let ![]() be a Quadrilateral such that the angles
be a Quadrilateral such that the angles ![]() and
and ![]() are Right Angles, then
are Right Angles, then ![]() is a cyclic quadrilateral (Dunham 1990). This is a Corollary of the theorem that, in a Right
Triangle, the Midpoint of the Hypotenuse is equidistant from the three Vertices.
Since
is a cyclic quadrilateral (Dunham 1990). This is a Corollary of the theorem that, in a Right
Triangle, the Midpoint of the Hypotenuse is equidistant from the three Vertices.
Since ![]() is the Midpoint of both Right Triangles
is the Midpoint of both Right Triangles ![]() and
and ![]() , it is
equidistant from all four Vertices, so a Circle centered at
, it is
equidistant from all four Vertices, so a Circle centered at ![]() may be drawn through them.
This theorem is one of the building blocks of Heron's
may be drawn through them.
This theorem is one of the building blocks of Heron's ![]() derivation of Heron's Formula.
derivation of Heron's Formula.
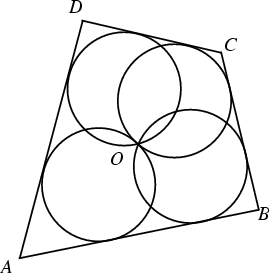
Place four equal Circles so that they intersect in a point. The quadrilateral ![]() is then a cyclic
quadrilateral (Honsberger 1991). For a Convex cyclic quadrilateral
is then a cyclic
quadrilateral (Honsberger 1991). For a Convex cyclic quadrilateral ![]() , consider the set of Convex cyclic
quadrilaterals
, consider the set of Convex cyclic
quadrilaterals ![]() whose sides are Parallel to
whose sides are Parallel to ![]() . Then the
. Then the ![]() of maximal Area is the one
whose Diagonals are Perpendicular (Gürel 1996).
of maximal Area is the one
whose Diagonals are Perpendicular (Gürel 1996).
See also Bretschneider's Formula, Concyclic, Cyclic Polygon, Cyclic Quadrangle, Euler Brick, Heron's Formula, Ptolemy's Theorem, Quadrilateral
References
Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 123, 1987.
Dunham, W. Journey Through Genius: The Great Theorems of Mathematics. New York: Wiley, p. 121, 1990.
Gürel, E. Solution to Problem 1472. ``Maximal Area of Quadrilaterals.'' Math. Mag. 69, 149, 1996.
Honsberger, R. More Mathematical Morsels. Washington, DC: Math. Assoc. Amer., pp. 36-37, 1991.
|
|
|
© 1996-9 Eric W. Weisstein