Fermat Point

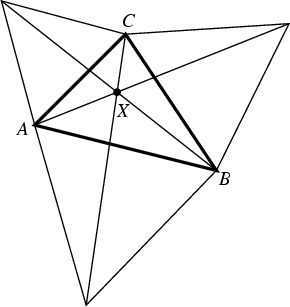
Also known as the first Isogonic Center and the Torricelli Point. In a given Acute Triangle $\Delta ABC$, the Fermat point is the point $X$ which minimizes the sum of distances from $A$, $B$, and $C$,

$$\vert AX\vert+\vert BX\vert+\vert CX\vert.$$ (1)

This problem is called Fermat's Problem or Steiner's Problem (Courant and Robbins 1941) and was proposed by Fermat to Torricelli. Torricelli's solution was published by his pupil Viviani in 1659 (Johnson 1929).

If all Angles of the Triangle are less than 120° ($2\pi/3$), then the Fermat point is the interior point $X$ from which each side subtends an Angle of 120°, i.e.,

$$\angle BXC = \angle CXA = \angle AXB = 120^\circ.$$ (2)

The Fermat point can also be constructed by drawing Equilateral Triangles on the outside of the given Triangle and connecting opposite Vertices. The three diagonals in the figure then intersect in the Fermat point. The Triangle Center Function of the Fermat point is

$$\alpha = \csc(A+{\textstyle{1\over 3}} \pi)$$ (3)

$$= bc[c^2a^2+(c^2+a^2-b^2)^2][a^2b^2-(a^2+b^2-c^2)^2][4\Delta-\sqrt{3}(b^2+c^2-a^2)].$$ (4)

The Antipedal Triangle is Equilateral and has Area

$$\Delta' = 2\Delta \left[{1+\cot\omega\cot\left({\pi\over 3}\right)}\right],$$ (5)

where $\omega$ is the Brocard Angle.

Given three Positive Real Numbers $l, m, n$, the ``generalized'' Fermat point is the point $P$ of a given Acute Triangle $\Delta ABC$ such that

$$l\cdot PA+m\cdot PB+n\cdot PC$$ (6)

is a minimum (Greenberg and Robertello 1965, van de Lindt 1966, Tong and Chua 1995)

See also Isogonic Centers

References

Courant, R. and Robbins, H. What is Mathematics?, 2nd ed. Oxford, England: Oxford University Press, 1941.

Gallatly, W. The Modern Geometry of the Triangle, 2nd ed. London: Hodgson, p. 107, 1913.

Greenberg, I. and Robertello, R. A. ``The Three Factory Problem.'' Math. Mag. 38, 67-72, 1965.

Honsberger, R. Mathematical Gems I. Washington, DC: Math. Assoc. Amer., pp. 24-34, 1973.

Johnson, R. A. Modern Geometry: An Elementary Treatise on the Geometry of the Triangle and the Circle. Boston, MA: Houghton Mifflin, pp. 221-222, 1929.

Kimberling, C. ``Central Points and Central Lines in the Plane of a Triangle.'' Math. Mag. 67, p. 174, 1994.

Kimberling, C. ``Fermat Point.'' http://cedar.evansville.edu/~ck6/tcenters/class/fermat.html.

Mowaffaq, H. ``An Advanced Calculus Approach to Finding the Fermat Point.'' Math. Mag. 67, 29-34, 1994.

Pottage, J. Geometrical Investigations. Reading, MA: Addison-Wesley, 1983.

Spain, P. G. ``The Fermat Point of a Triangle.'' Math. Mag. 69, 131-133, 1996.

Tong, J. and Chua, Y. S. ``The Generalized Fermat's Point.'' Math. Mag. 68, 214-215, 1995.

van de Lindt, W. J. ``A Geometrical Solution of the Three Factory Problem.'' Math. Mag. 39, 162-165, 1966.