Ford Circle

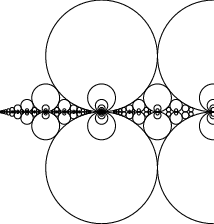
Pick any two Integers $h$ and $k$, then the Circle of Radius $1/(2k^2)$ centered at $(h/k, \pm 1/(2k^2))$ is known as a Ford circle. No matter what and how many $h$s and $k$s are picked, none of the Ford circles intersect (and all are tangent to the x-Axis). This can be seen by examining the squared distance between the centers of the circles with $(h,k)$ and $(h',k')$,

$$d^2=\left({{h'\over k'}-{h\over k}}\right)^2+\left({{1\over 2k'^2}-{1\over 2k^2}}\right).$$ (1)

Let $s$ be the sum of the radii

$$s=r_1+r_2={1\over 2k^2}+{1\over 2k'^2},$$ (2)

then

$$d^2-s^2={(h'k-hk')^2-1\over k^2k'^2}.$$ (3)

But $(h'k-k'h)^2\geq 1$, so $d^2-s^2\geq 0$ and the distance between circle centers is $\geq$ the sum of the Circle Radii, with equality (and therefore tangency) Iff $\vert h'k-k'h\vert=1$. Ford circles are related to the Farey Sequence (Conway and Guy 1996).

See also Adjacent Fraction, Farey Sequence, Stern-Brocot Tree

References

Conway, J. H. and Guy, R. K. ``Farey Fractions and Ford Circles.'' The Book of Numbers. New York: Springer-Verlag, pp. 152-154, 1996.

Ford, L. R. ``Fractions.'' Amer. Math. Monthly 45, 586-601, 1938.

Pickover, C. A. ``Fractal Milkshakes and Infinite Archery.'' Ch. 14 in Keys to Infinity. New York: W. H. Freeman, pp. 117-125, 1995.

Rademacher, H. Higher Mathematics from an Elementary Point of View. Boston, MA: Birkhäuser, 1983.