|
|
|
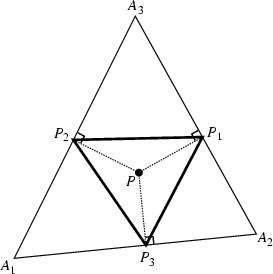
Given a point ![]() , the pedal triangle of
, the pedal triangle of ![]() is the Triangle whose Vertices are the feet of
the perpendiculars from
is the Triangle whose Vertices are the feet of
the perpendiculars from ![]() to the side lines. The pedal triangle of a Triangle with Trilinear Coordinates
to the side lines. The pedal triangle of a Triangle with Trilinear Coordinates
![]() and angles
and angles ![]() ,
, ![]() , and
, and ![]() has Vertices with Trilinear Coordinates
has Vertices with Trilinear Coordinates
|
|
(1) |
|
|
(2) |
|
|
(3) |
The third pedal triangle is similar to the original one. This theorem can be generalized to: the ![]() th pedal
th pedal ![]() -gon of any
-gon of any
![]() -gon is similar to the original one. It is also true that
-gon is similar to the original one. It is also true that
| (4) |
| (5) |
See also Antipedal Triangle, Fagnano's Problem, Pedal Circle, Pedal Line, Schwarz's Triangle Problem
References
Coxeter, H. S. M. and Greitzer, S. L. Geometry Revisited. Washington, DC: Math. Assoc. Amer., pp. 22-26, 1967.
Johnson, R. A. Modern Geometry: An Elementary Treatise on the Geometry of the Triangle and the Circle. Boston, MA: Houghton Mifflin, 1929.